Diferencia entre revisiones de «Pronósticos»
Ir a la navegación
Ir a la búsqueda
(3 modelos) |
Sin resumen de edición |
||
| (No se muestran 2 ediciones intermedias del mismo usuario) | |||
| Línea 7: | Línea 7: | ||
!BIBLIOGRAFIA | !BIBLIOGRAFIA | ||
|- | |- | ||
| | |Metodo | ||
Arimas | |||
| | |Concepto Metodo ARIMA | ||
Modelos ARIMA (Autoregressive Integrated Moving Average) son una herramienta poderosa en el análisis de series temporales, utilizada para predecir futuros valores basándose en datos históricos. | |||
El modelo ARIMA combina tres componentes: | El modelo ARIMA combina tres componentes: | ||
# | # Autorregresivo (AR): Utiliza las dependencias entre una observación y un número de observaciones anteriores. | ||
# | # Integrado (I): Involucra la diferenciación de las observaciones para hacer la serie temporal estacionaria. | ||
# | # Media Móvil (MA): Modela el error de predicción como una combinación lineal de errores de predicción pasados. | ||
El modelo se denota como ARIMA(p, d, q), donde: | El modelo se denota como ARIMA(p, d, q), donde: | ||
| Línea 46: | Línea 28: | ||
|[[Archivo:Img3.png|miniaturadeimagen]] | |[[Archivo:Img3.png|miniaturadeimagen]] | ||
|[https://statologos.com/arima/ Enlace Bibliografia] | |[https://statologos.com/arima/ Enlace Bibliografia] | ||
|- | |||
|Modelo de Monte Carlo | |||
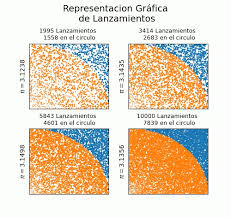
|El modelo de Monte Carlo utiliza simulaciones para predecir el comportamiento de sistemas complejos. Se generan miles o incluso millones de simulaciones utilizando valores aleatorios dentro de distribuciones de probabilidad asignadas a las variables clave. Esto permite evaluar la probabilidad de diversos resultados y tomar decisiones informadas en entornos inciertos | |||
|En la gestión de proyectos, el modelo de Monte Carlo se utiliza principalmente para: | |||
# '''Evaluar el Riesgo''': Ayuda a identificar y cuantificar los riesgos asociados con diferentes aspectos del proyecto, como el cronograma y el presupuesto. | |||
# '''Pronosticar Plazos y Costos''': Permite prever la probabilidad de cumplir con los plazos y presupuestos establecidos, considerando las incertidumbres y variabilidades. | |||
# '''Optimizar Decisiones''': Facilita la toma de decisiones estratégicas al proporcionar un análisis detallado de los posibles resultados y sus probabilidades | |||
|[[Archivo:Image12.png|miniaturadeimagen]] | |||
|[https://www.questionpro.com/blog/es/simulacion-de-monte-carlo/ Enlace Bibliografia] | |||
|- | |||
|Modelos de Series de Tiempo | |||
|Analizan la evolución de una variable a lo largo del tiempo, identificando patrones como tendencias, estacionalidad y ciclos. | |||
| | |||
# Estimación de duración de tareas: Pronosticar el tiempo necesario para completar una tarea en función de datos históricos de proyectos similares. | |||
# Predicción de costos: Estimar los costos futuros de un proyecto basándose en el gasto histórico. | |||
|[[Archivo:Image.png|miniaturadeimagen]] | |||
|[https://bookdown.org/content/2274/series-temporales.html Enlace bibliografia] | |||
|} | |} | ||
Revisión actual - 19:53 12 ago 2024
| CONCEPTO | CONCEPTO | APLICACION | IMAGEN | BIBLIOGRAFIA |
|---|---|---|---|---|
| Metodo
Arimas |
Concepto Metodo ARIMA
Modelos ARIMA (Autoregressive Integrated Moving Average) son una herramienta poderosa en el análisis de series temporales, utilizada para predecir futuros valores basándose en datos históricos. El modelo ARIMA combina tres componentes:
El modelo se denota como ARIMA(p, d, q), donde:
|
|
Enlace Bibliografia | |
| Modelo de Monte Carlo | El modelo de Monte Carlo utiliza simulaciones para predecir el comportamiento de sistemas complejos. Se generan miles o incluso millones de simulaciones utilizando valores aleatorios dentro de distribuciones de probabilidad asignadas a las variables clave. Esto permite evaluar la probabilidad de diversos resultados y tomar decisiones informadas en entornos inciertos | En la gestión de proyectos, el modelo de Monte Carlo se utiliza principalmente para:
|
Enlace Bibliografia | |
| Modelos de Series de Tiempo | Analizan la evolución de una variable a lo largo del tiempo, identificando patrones como tendencias, estacionalidad y ciclos. |
|
Enlace bibliografia |