Diferencia entre revisiones de «Análisis mediante árbol de decisiones»
(Página creada con «Índice Concepto Aplicación Pasos para Realizar el Análisis mediante Árbol de Decisiones Ejemplo Imagen Referencial Referencias Recursos Adicionales Fórmulas y Recursos Explicativos Adicionales…») |
Sin resumen de edición |
||
| (No se muestran 4 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
{| class="wikitable" | |||
|- | |||
! Concepto !! Aplicación !! Imagen referencial !! Fuente Bibliográfica | |||
|- | |||
| | |||
El análisis mediante árbol de decisiones es una herramienta de gestión de proyectos que ayuda a tomar decisiones informadas considerando diferentes alternativas y sus posibles consecuencias. Un árbol de decisiones es un diagrama que representa diferentes decisiones y sus posibles resultados, incluyendo eventos de incertidumbre, costos, utilidades y riesgos. | |||
Fórmula para calcular el valor esperado (VE): | |||
<math> | <math> | ||
VE = \sum (P_i \times V_i) | VE = \sum (P_i \times V_i) | ||
</math> | </math> | ||
Donde: | Donde: | ||
* \( P_i \) = Probabilidad de cada resultado | |||
* \( V_i \) = Valor del resultado | |||
|| | |||
El análisis mediante árbol de decisiones se aplica en diferentes etapas de la gestión de proyectos según PMBOK7, especialmente en los procesos de: | El análisis mediante árbol de decisiones se aplica en diferentes etapas de la gestión de proyectos según PMBOK7, especialmente en los procesos de: | ||
* Planificación de la Gestión de Riesgos: Identificación y análisis de riesgos, así como la planificación de respuestas a los riesgos. | |||
* Análisis Cuantitativo de Riesgos: Evaluación de los efectos combinados de los riesgos e incertidumbres en los objetivos del proyecto. | |||
* Desarrollo del Caso de Negocio: Evaluación de las diferentes alternativas estratégicas para justificar la inversión en el proyecto. | |||
Pasos para Realizar el Análisis mediante Árbol de Decisiones: | |||
# Definición del Problema: Identificar claramente el problema o decisión a analizar. | |||
# Identificación de Alternativas: Listar todas las posibles alternativas o decisiones que se pueden tomar. | |||
# Construcción del Árbol de Decisiones: Dibujar el árbol de decisiones incluyendo las alternativas, los eventos inciertos y sus posibles resultados. | |||
# Asignación de Probabilidades: Asignar probabilidades a los diferentes eventos inciertos. | |||
# Estimación de Resultados: Asignar valores o resultados a cada combinación de decisiones y eventos inciertos. | |||
# Cálculo del Valor Esperado: Calcular el valor esperado para cada rama del árbol de decisiones utilizando la fórmula del valor esperado. | |||
# Análisis y Selección: Analizar los resultados y seleccionar la alternativa con el mayor valor esperado o que mejor se alinee con los objetivos del proyecto. | |||
Ejemplo: | |||
Supongamos que un proyecto tiene dos alternativas: A y B. La alternativa A tiene un 50% de probabilidad de generar $100,000 de beneficio y un 50% de probabilidad de generar $50,000. La alternativa B tiene un 70% de probabilidad de generar $80,000 y un 30% de probabilidad de generar $30,000. | Supongamos que un proyecto tiene dos alternativas: A y B. La alternativa A tiene un 50% de probabilidad de generar $100,000 de beneficio y un 50% de probabilidad de generar $50,000. La alternativa B tiene un 70% de probabilidad de generar $80,000 y un 30% de probabilidad de generar $30,000. | ||
Para la alternativa A: | Para la alternativa A: | ||
<math> | <math> | ||
VE_A = (0.5 \times $100,000) + (0.5 \times $50,000) = $75,000 | VE_A = (0.5 \times \$100,000) + (0.5 \times \$50,000) = \$75,000 | ||
</math> | </math> | ||
Para la alternativa B: | Para la alternativa B: | ||
<math> | <math> | ||
VE_B = (0.7 \times $80,000) + (0.3 \times $30,000) = $65,000 | VE_B = (0.7 \times \$80,000) + (0.3 \times \$30,000) = \$65,000 | ||
</math> | </math> | ||
En este caso, la alternativa A tendría un mayor valor esperado y sería la elección preferida según el análisis mediante árbol de decisiones. | En este caso, la alternativa A tendría un mayor valor esperado y sería la elección preferida según el análisis mediante árbol de decisiones. | ||
|| | |||
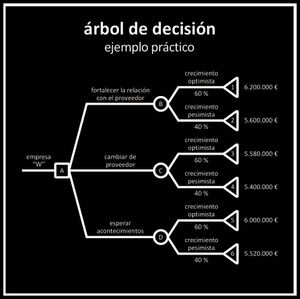
[[File:arbol.jpg|300px|Arbol de decisión]] | |||
[[File | || | ||
. | * Project Management Institute. (2021). A Guide to the Project Management Body of Knowledge (PMBOK® Guide) – Seventh Edition. Newtown Square, PA: Project Management Institute. | ||
* Investopedia. (2023). Decision Tree. [https://www.investopedia.com/terms/d/decision-tree.asp Investopedia] | |||
* Clemen, R. T., & Reilly, T. (2013). Making Hard Decisions with DecisionTools. Cengage Learning. | |||
* Schwalbe, K. (2019). Information Technology Project Management. Cengage Learning. | |||
* Berman, K., & Knight, J. (2013). Financial Intelligence for Entrepreneurs: What You Really Need to Know About the Numbers. Harvard Business Review Press. | |||
* ScienceDirect. (2023). Decision Analysis in Project Management. [https://www.sciencedirect.com/science/article/pii/S0263237318300385 ScienceDirect] | |||
|} | |||
Revisión actual - 19:46 16 ago 2024
| Concepto | Aplicación | Imagen referencial | Fuente Bibliográfica |
|---|---|---|---|
|
El análisis mediante árbol de decisiones es una herramienta de gestión de proyectos que ayuda a tomar decisiones informadas considerando diferentes alternativas y sus posibles consecuencias. Un árbol de decisiones es un diagrama que representa diferentes decisiones y sus posibles resultados, incluyendo eventos de incertidumbre, costos, utilidades y riesgos. Fórmula para calcular el valor esperado (VE): Donde:
|
El análisis mediante árbol de decisiones se aplica en diferentes etapas de la gestión de proyectos según PMBOK7, especialmente en los procesos de:
Pasos para Realizar el Análisis mediante Árbol de Decisiones:
Ejemplo: Supongamos que un proyecto tiene dos alternativas: A y B. La alternativa A tiene un 50% de probabilidad de generar $100,000 de beneficio y un 50% de probabilidad de generar $50,000. La alternativa B tiene un 70% de probabilidad de generar $80,000 y un 30% de probabilidad de generar $30,000. Para la alternativa A: Para la alternativa B: En este caso, la alternativa A tendría un mayor valor esperado y sería la elección preferida según el análisis mediante árbol de decisiones. |
|